Life Would be Easier if We Did Not Need to Make Predictions

Actuaries are sometimes assumed to have magical forecasting powers.

A few years ago, I was asked to develop a 10-year cost model for a program. After some discussion, it became clear this was a program that did not yet have a target population (so size could vary over an order of magnitude), a service model (so how much staff time would be needed per person) nor a delivery model (unclear who would be managing the program and front-line staff). The client was surprised when we would struggle to get any estimates that were not subject to massive uncertainty.

Part of the profession’s skillset is to communicate uncertainty (or in the case of this article, our uncertainty about our uncertainty!). But it does mean walking the line between pushing back, given the uncertainty, or producing uncertain estimates (on the basis that no one else is better positioned to provide them).

At this year’s Summit , there was a session by Adrian McGarva and Don Johnstone around APRA’s capital standards under GPS 116, including the Insurance Concentration Risk Charge. One thing arising from the discussion is APRA’s use of 1 in 200-year events (or 0.5% probability of occurrence) as a test for capital adequacy. This applies to natural period losses as well as other accumulations.

Viewed heuristically, the requirement is very helpful; it requires a careful consideration of extreme risks that could affect an insurer. Similar regulations in other countries recommend using historical events as inspiration – what would a Global Financial Crisis, or a pandemic, or a Great Depression do to an insurance portfolio? This is effective in pushing outside the narrow variation of risk we see most years.

However, if we move to a formal statistical lens, problems rapidly arise (accumulate, perhaps?):

• Extremes of statistical distributions are difficult to estimate. While theorems like the central limit theorem guarantee good convergence for central estimates such as the mean, similar levels of accuracy at an extreme require much more data.
• The underlying distribution is unknown. If we knew that losses followed a particular distribution (e.g. normal), then we could leverage our knowledge of smaller losses to understand larger ones. In reality, the tail risk tends to be its own beast.
• We do not have much history, and it evolves. Good statistical estimation requires a large number of independent and identically distributed draws. However, the world and our insurance portfolio change over time – and will continue to do so in the future. And having a few decades of data would be considered luxurious. This means we will struggle to infer from actual history.

It is hard to communicate the extent of this plight using real data, as every company is complex and different. But we can take a purely statistical approach (code is here). Suppose we assume our portfolio loss (in $m) is lognormally distributed with a mean of $279m, and standard deviation of $313m (so relatively high risks of large losses). Assume further that we have 100 years of experience (data points) from which to estimate tails from, and that we only want to use the top 10% of losses to estimate the tail shape (as it may differ from the rest of the distribution). A popular approach is to fit a generalised Pareto distribution to the tail, consistent with extreme value theory.

We run the experiment 10,000 times (full code available here ) and look at our estimate of the 99.5^th percentile compared to the true level. The resulting histogram is shown – each point on the histogram is a formal estimate of the 99.5^th percentile loss.

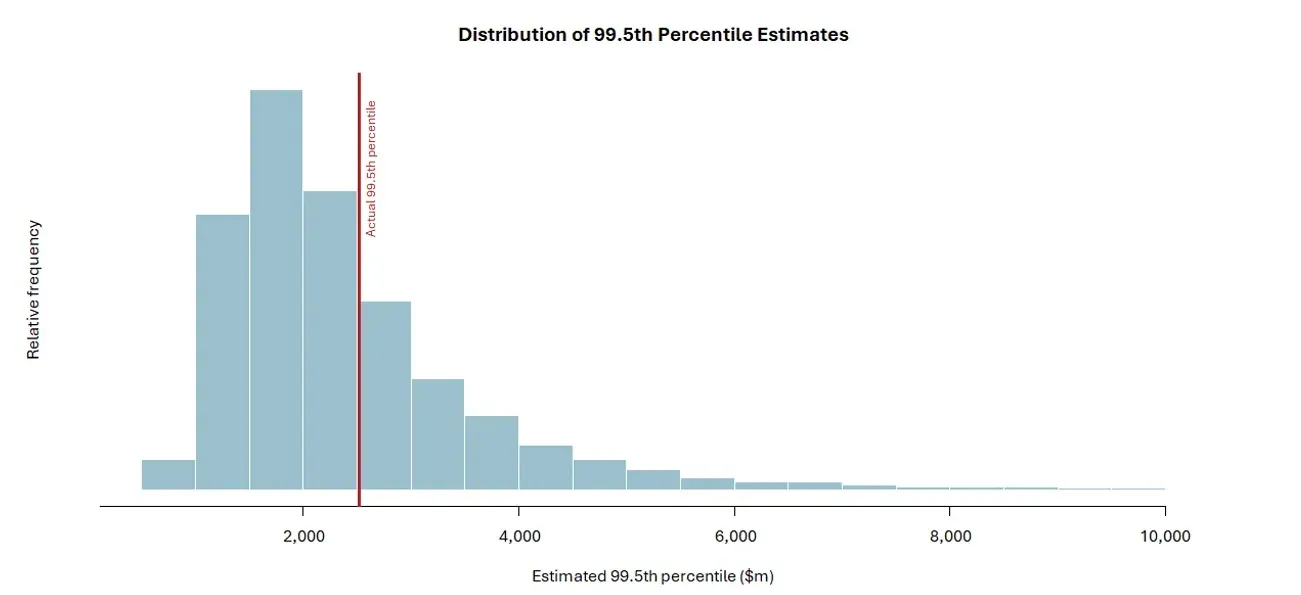
Hopefully, the main finding is clear – estimating the percentile is very hard off 100 data points. The 95% range of estimates is ($1,030m, $6,180m), which means that you could plausibly have estimates that are six times larger than others, depending on statistical noise alone. An actuary reporting $1,030m would actually only be reporting the 96^th percentile, while another reporting $6,180 would have 99.95% sufficiency. This variability in potential results does not feel unusual for this type of estimate.

What does this mean?

I think it puts actuaries in an interesting position where we are required by regulation to make estimates that carry an enormous amount of uncertainty. It relies on experience and judgement to then appropriately communicate that uncertainty and resist the temptation to use the uncertainty as an excuse for lowering estimates. A related challenge is year-on-year volatility; formal estimation every year would probably create significant volatility, but our insurance company may not be grateful for this.

It also makes me worry a little that we’re magically producing the rabbit of statistical certainty from an empty hat.