IFRS 17: Discounting and Market Complexities

A sum of money currently available has a greater value than the same sum to be paid in the future, due to its earnings potential in the interim. This so-called “Time Value of Money” is a core principle of finance, which is also reflected in IFRS 17. Therefore, suitable discount rates shall be applied to the projected future cash flows.

According to IFRS 17, appropriate discount rates applied to the estimates of future cash flows shall (see IFRS 17 paragraph 36):

• Reflect the time value of money, the characteristics of the cash flows and the liquidity characteristics of the insurance contracts.
• Be consistent with observable current market prices (if available) for financial instruments with cash flows whose characteristics are consistent with those of the insurance contracts, e.g. in terms of timing, currency, and liquidity.
• Exclude the effect of any factors influencing such observable market prices that do not affect the future cash flows of the insurance contracts.

Basis rules to derive discount rates

Under Solvency II, the Matching Adjustment (MA) enables insurers to adjust the risk-free interest rate used for discounting specific long-term insurance liabilities. This adjustment incorporates the illiquidity premium associated with holding less liquid assets that are closely aligned with the cash flows of these liabilities.

In contrast, IFRS 17 does not impose explicit restrictions on the selection of the reference portfolio. Insurers have the flexibility to utilise their own asset portfolios, provided the resulting discount rates appropriately reflect the characteristics of the insurance contracts and are consistent with observable market data.

Furthermore, similar to the Volatility Adjustment in Solvency II, discount rates can also be derived, starting from risk-free rates and adding an allowance for illiquidity.

We, therefore, end up with two approaches to set the discount rate, namely “top-down” and “bottom-up” (see IFRS 17 paragraph B80/B81):

• The top-down approach is based on a yield curve that reflects the current market rates of return implicit in a fair value measurement of a reference portfolio of assets and adjusted to eliminate any factors that are not relevant to the insurance contracts.
• The bottom-up approach is based on adjusting a liquid risk-free yield curve to reflect the differences between the liquidity characteristics of the financial instruments that underlie the risk-free rates observed in the market and the liquidity characteristics of the insurance contracts.

Example: 

Most companies are using the bottom-up approach – in many cases, very closely to the Volatility Adjustment used in Solvency II. However, there are some exceptions, for example:

• Aegon has generalised the two approaches into one unified direct discounting technique in which discount rates are determined as the sum of the risk-free rate plus a percentage of the (product-specific) illiquidity premium.
• Aviva and Phoenix (UK) use the top-down approach for annuities (where they also apply the Matching Adjustment in Solvency II).

Cash flows that vary based on the returns on any financial underlying items (e.g. when applying the Variable Fee Approach (VFA) for direct participating business) shall be:

• discounted using rates that reflect that variability; or
• adjusted for the effect of that variability and discounted at a rate that reflects the adjustment made.

Option (i) could be analogous to a real-world valuation framework, which is concerned with producing a realistic view of potential future economic variables. In this framework, the discount rates for cash flows that vary would reflect the rates of return used to project the underlying items on a real-world basis (asset-based discount rates).

Option (ii) permits a rate of return on underlying items that is not necessarily a real-world framework, with cash flows adjusted to be consistent. This framework relies on mathematical relationships within and among financial instruments and could include a risk-neutral valuation where risk-free rates of return (with or without liquidity premium) are used to project the underlying items and to discount the cash flows.

Challenges

A notable challenge faced by many insurers is the duration and yield mismatch (own portfolio versus market-referenced portfolio), where long-dated liabilities are paired with medium-term matching assets. In such situations, the application of a liquidity premium based on the entity’s own portfolio can lead to meaningful outcomes:

• Scenario 1: If the insurer holds highly illiquid assets with long-term horizons, these assets typically offer yields and coupons significantly above market averages. Consequently, the discount rate applied to the insurance liabilities would be higher, leading to lower reported liabilities.
• Scenario 2: Conversely, if the insurer has invested in low-yield assets in a high-interest-rate environment, the discount rate would be lower, resulting in higher reported liabilities.

Furthermore, currency and term mismatches introduce additional complexities, particularly in product lines such as annuities or whole-of-life contracts, where the liability durations often exceed the maturity profiles of the available matching assets.

Concrete implementation

The Canadian Institute of Actuaries has issued an Educational Note on how to derive the IFRS 17 discount rates in practice ^[1] :

• Establishing the last observable point on the yield curve: observable market prices would be used where available in active markets.
• Setting the ultimate risk-free rate: an actuary shall develop unobservable inputs using the best information available and might place more weight on long-term estimates than on short-term fluctuations.
• Setting the liquidity premium: the discount rates would reflect the characteristics of the insurance contracts, including liquidity.
• Setting the discount rates for products containing cash flows that vary with an underlying item.

The last observable point for risk-free discount rates would correspond to the term of the asset with the longest maturity for which there is a quoted price from an active market (a market in which transactions for an asset take place with sufficient frequency and volume to provide pricing information on an ongoing basis). To assess whether there is a sufficient frequency of transactions for risk-free assets in the market, factors such as bid-ask spread, trading volume, trade size, and the impact of trades must be considered.

When setting the discount curve beyond the last observable point, the following characteristics may be desirable:

• Stability: the ultimate interest rate would be more stable over time (on average, one might expect the variability of long-term interest rates to be lower than short-term rates).
• Smoothness: interpolated rates would follow a smooth path from the last observable point to the ultimate long-term rate.
• Simplicity: the approach would be easy to understand and implement.

Setting the liquidity premium is not straightforward. Market-based techniques use the spread difference between covered bonds and risk-free bonds in the same currency to directly derive the liquidity premium. However, due to missing liquidity and longer-term durations of the corresponding instruments, this approach may not be feasible in many markets.

The discount rates most European companies are using are based on the Solvency II discount rates, which are consistent with IFRS 17. Their Euro rates are normally based on market rates up to 30 years – in contrast to the EIOPA rates, where the extrapolation to the ultimate forward rate starts much earlier. As a result, they are expected to react more in line with the asset movements. For portfolios with less liquid liabilities (e.g., annuities in payment), they add significant illiquidity premiums. However, for portfolios measured with the Variable Fee Approach (VFA), they use more conservative discount rates.

In many developing markets, companies are struggling to determine discount rates based on observable market data. Risk-free rates do not exist, and neither do long-term investments: the longest duration may be a few years or even less than a year.

In such cases, applying any sophisticated methodology as the one mentioned above, does not make sense. The only reference point can be the long-term investment return the company can achieve, deducting an allowance for unexpected losses. An exception are countries whose currency is pegged to the US dollar or another lead currency with long-term rates; in this case, the companies usually take those rates as a starting point.

Changing discount rates

For each accounting period, the discount rates have to be updated in line with market movements – as companies are required to use current assumptions. For long-term liabilities, this can have a significant impact on the time value of money and, as a result, on the fulfilment of cash flows.

Companies can determine in their accounting policy whether the effect of changes in market discount rates are recognised in P&L or in Other Comprehensive Income (OCI), in the latter case with interest accrued to the P&L at the discount rate locked in at inception.

At first glance, OCI seems to be the better choice as the volatility stemming from updated discount rates should not distort the P&L. However, the change in the fair value of some assets, particularly the ones used for interest rate hedging, is always flowing through the P&L. Therefore, a careful analysis should be made to decide which choice is appropriate for a specific company.

Observations

In the Solvency II environment, the discount rates published by EIOPA are a natural reference point. 42% of the respondents in a survey by EIOPA reported using the same or almost the same rates. The remaining 58% used in most cases a higher discount rate than Solvency II. ^[2]

58.5% use the same risk-free rate as in Solvency II; for those not using the same rate, the most relevant differences are a more remote last liquid point (e.g. 30 years for Euro) and a different ultimate forward rate.

There are some further observations from analysing the 2024 annual reports:

• In developing markets with local currencies pegged to USD, companies normally use the USD rates with a particular uplift.
• Some companies vary the discount rates by product type. In many cases, the discount rates for annuities in payment are significantly higher than thoseusually derived from the yield of the asset portfolio backing the specific liabilities (“top-down”) and with a higher illiquidity premium.
• Many companies use different rates for the General Model (GMM) and the Premium Allocation Approach than for the VFA with VFA rates being more conservative.
• The disclosures of the discount rates vary by company. Most companies indicate the rates used for certain durations (e.g., 1, 5, 10, 20, 30 years), some even publishing an ultimate rate for exceptionally long durations, others just publish a range (either by duration buckets or overall).

The spreads in the discount rates used by sample companies vary significantly as shown in the following graphs for year-end 2024, comparing the discount rates with the risk-free rate published by EIOPA for Solvency II purposes.

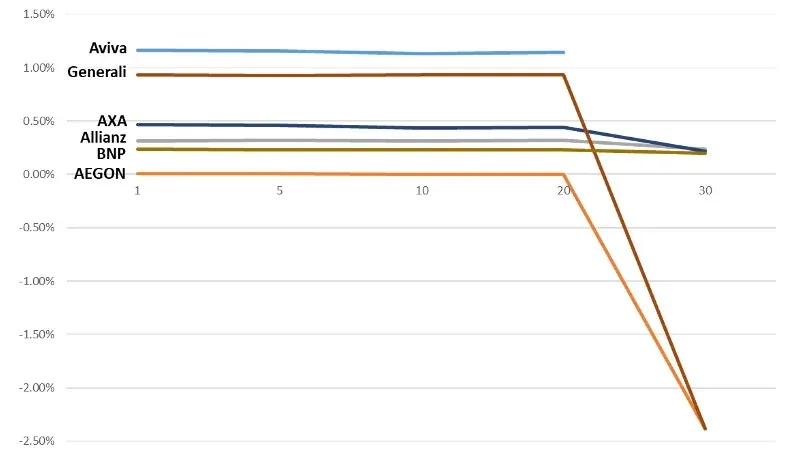
2024: EUR spread over EIOPA risk-free | Source: Published Financial Statements as of December 31, 2024

The spreads in EUR are pretty constant but seem to drop for durations longer than 20 years; however, this is rather an artificial result stemming from different extrapolation methods for long durations (the EIOPA rates converging to the so-called Ultimate Forward Rate).

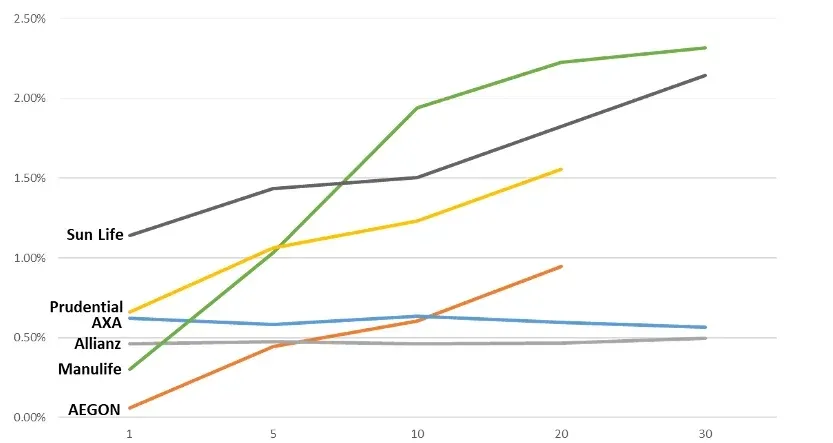
2024: USD spread over EIOPA risk-free | Source: Published Financial Statements as of December 31, 2024

The spreads in USD used by the different companies seem to increase with duration in most cases (however, several companies do not disclose discount rates for long durations).

There are companies that decided in the first place to use some average rates for their interest-sensitive business which were not accurately reflecting the actual pricing rates for the various cohorts. This seemed to be a reasonable simplification, given the administrative burden of maintaining multiple sets of yield curves over time. However, they noticed that, in many cases, many cohorts turned out to be onerous despite having reasonable pricing margins in reality.

Therefore, we would highly recommend analysing the quantitative impact of particular “simplifications” at the earliest possible stage.

For a deeper understanding of the discount rate and its impact on actuarial models and accounting, explore the insights offered in the book Navigating IFRS 17: A Practical Guide to Accounting & Actuarial Implementation , which is authored by the authors of this article.

References

^[1] Canadian Institute of Actuaries Educational Note / IFRS 17 Discount Rates for Life and Health Insurance Contracts, June 2020: https://www.cia-ica.ca/publications/224099e/

^[2] EIOPA: “IFRS 17 – Insurance contracts report”, April 2024